The Art and Practice of Content Assembly: Where IA and CMS Meet

There’s a murky space where Information Architecture and Content Management meet. This is a God-forsaken back alley where dirty deals are negotiated and where idealism and purity go to die. This is the place were your wireframes are sacrificed on the altar of your CMS.

The most common cause of death? Managing content assembly, which is the seemingly simple concept of getting multiple items of content into a group (an “assembly” – it’s both a noun and verb, in this usage; I’m stealing this from a decades-old Documentum concept).

The reason for grouping content together is usually always in order to have this content appear in the same location on your website.

This is trivial right? I mean, this happens all the time on every website.:

1. A department subsite menu with a bunch of resources specific to that department explicitly placed in a hierarchy.

2. A blog with a group of blog posts ordered from latest to oldest.

3. A topic page about something with a bunch of disparate resources all related to that topic in order of relevance as determined by a content retrieval algorithm.

4. A set of “related content” links under an article.

5. A list of the “Latest News” headlines on the home page.

Wireframes are great for this – “we’re going to have this menu here, and these links here, and some related content over here…” etc. Information Architects just go crazy with this stuff, and they really should because that’s their job.

Sadly, my job is to make all that stuff work. When I see any listing of content in any form on a wireframe, I’m automatically thinking “how am I going to get that content to appear in that spot within the capabilities of this CMS?”

Doing this is so fundamental to any website that you might be saying, “well, sure…” But, when you dig into it, the ability (or inability) for a CMS to do this is a critical differentiator. And unless your site is like Wikipedia, essentially consisting of a single content item displayed with nothing other than intra-text navigation (hint: it’s not), then a huge part of integrating a CMS is figuring out how to associate content together in such a way that it can be displayed correctly.

If you’re a regular reader of Gadgetopia, then you might be thinking:

• Wait, isn’t this just relational content modeling? There’s certainly some overlap, but not really. With relational modeling, you’re figuring out how Content X is specifically linked to Content Y, often via a referential property – like an Article having an Author property which links to an Author object. The link is usually direct from X to Y.

• Wait, isn’t this just content geography? That’s one method of assembly, yes (see below). But there are several others. (If you haven’t read that post, go do it now. A lot of the stuff below will make more sense if you understand the concept of content geography.)

In a general sense, content assembly is about grouping content together into assemblies. These assemblies often have no relationship to your core content geography. They exist apart from and in addition to it. They are “mini” or “alternate” geographies.

(Note that content assembly isn’t concerned with intra-text linking. You can always just have a WYSIWYG field and let editors create whatever links and content they want in there. But to do that is to completely remove any benefit of having a CMS in the first place.)

That term – “assembly” – is purposely vague. An assembly could be anything – a category, a parent content object, a keyword, a query based on some property, etc. The operative idea is simply that you have something to which you can refer that will return multiple content objects, optionally in some specific sequence or internal organization.

Take this for example (lifted from a random wireframe I had on my laptop):

This is a simple image carousel, right? Sure, but in a generic sense, it’s also an assembly of content. And, as such, it presupposes a few things:

1. You have some assembly that will return exactly four content items. (The carousel might allow overflow, so perhaps this won’t matter.)

2. This assembly will restrict itself to content that will render correctly. In this case, it needs to be either a dedicated “Carousel Image” content object or some kind of content interface that always has a title, a subtitle, and an image.

3. You can put this content in an arbitrary order. Items in the carousel are lined up from left to right, and if you want Content X to the left of Content Y, you need to be able to specify this.

4. It likely has some permissions attached to it. This particular carousel was on the home page of the site, and one does not simply walk into Mordorand all that…

5. What about workflow? The key here is subtle – there will likely be approval workflow on the individual items, because they exist on their own as news items or whatever. But there might also need to be workflow on the assignment to the image carousel itself, completely separate from workflow around them existing as news articles not in the carousel.

And these are just the raw technical requirements. You also have to consider how usable this process will be for the editors. Will they understand the method you come up with, or that your CMS offers? What training will be required to get them to understand how it works?

As a content management integrator, your time with wireframes is mostly spent answering questions like these:

1. What assemblies are needed to render the content the way the wireframes dictate?

2. Do the assemblies themselves need to be structured, either to have metadata attached to them, or related to each other in some way? Are they flat or hierarchical?

3. Do the assemblies need any restrictions on content types, minimum members, or maximum members?

4. Once the assemblies are identified, how will the content get “inside” of them? Is it an explicit assignment, or is their membership in a particular assembly derived from data or geography?

5. Inside of a specific assembly, does the content need to be ordered in any specific way, or is it enough to just be an unordered bucket?

6. Do the assemblies need to have any security considerations, either for placing content into them, or reading content out of them?

7. Are certain assemblies mutually exclusive? Does the existence of content inside Assembly X mean it can’t be in Assembly Y? Alternately, does content need to appear in more than one substructure in a larger overall assembly?

8. Will the assembly return the content in a raw, unaltered format? Or does it change the content in some way?

Note that all of these questions pretty much have to be answered with a CMS in mind because the answers will be different for every CMS. Remember when I said that this is where IA and CMS meet? It’s true – this is where the rubber hits the road. This is the moment where you realize whether your CMS is up to task or not.

(Can any non-specific-CMS generalities be made about this discipline? Yes, and most of them are in this post. I don’t say that to pump up the importance of this post, but rather to reinforce the fact that there are precious-few generalities in this space. The discipline of content assembly is directly at the intersection of IA and a specific CMS.)

With any CMS, there are usually a bunch of ways to do this, and the more options you have, the better, because each method has advantages and drawbacks.

Here’s a brief survey of some of the more common methods of content assembly.

Content Geography

In this situation, you put content in specific locations – you have an explicit geography which you use to place content. The existence of content in a specific location with other content is what binds it together. For example, you have a location in your content structure for Topic X. You put all content related to Topic X in this location.

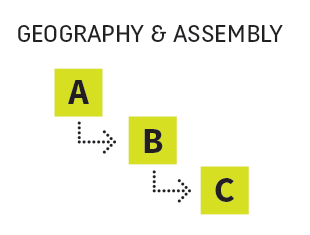
In this case, our content geography and our assembly are the same thing.

Geography as an assembly seems a little odd, because systems with a strong geography make it so core that it doesn’t come across as a “mere” assembly method, but it fits all the characteristics of one, both in theory and practice.

It has benefits and drawbacks:

• You get an inherent parent-child relationship between the assembly and the content (assuming a tree, which 99% of geographies are). If the assembly is the parent, and the content is the child, then content is a descendant of the assembly, and there’s an enormous amount of functionality this enables.

• It integrates well with permissions. Permissions usually always run off geography, so certain editors can have access to the Topic X area and put content in there. Other editors might not have access.

• You can often explicitly order things inside the geography, putting them in a desired sequence.

• If your CMS has a decent content tree, there’s often an implicit taxonomy. If Topic Y is inside Topic X, then Topic X can theoretically “roll-up” content in both – show content from both X and Y – if desired.

• It makes intuitive sense to a lot of editors. You have a place for everything, and everything goes in its place. The idea of content “living” in a specific place is something that editors can wrap their heads around easily.

• The topic is itself a content object, likely. You’ll have a “Section” or “Topic” content object, which makes a lot of things easier – you can link to it, you can add data to it, you can render it, etc. (See: Using Proxy Objects for Non-CMS Content for more on this.)

• Deleting the assembly (the parent content object, in most cases) deletes the content. Is this a benefit or a drawback? Could be both, depending on what you want.

• Multi-assembly assignment might be hard. What if Content X fits both Topic X and Topic Y? Some systems make it easy for content to appear in both places, some make it hard. What if Topic Y cuts completely across the classification tree? What if it transcends the classification tree completely? How do you do that?

• Adding topics might be hard. You’re not just just adding a keyword or category – you’re altering the content structure of the system.

• It tends to bind your IA to your content structure. In some situations, this is a great, in others it’s not. (Some IAs, in particular, are horrified by this idea. IA is a pure and beautiful thing, not to be sullied by content structure.)

Structured Categorization

With this, you assign content to existing categories (really, just generic assemblies, but we’ll call them “categories” here since that’s a much more relatable term)

These categories exist in a separate structure, most often a list or tree. You check a series boxes or something to put Content X in Topics X, Y, and X. The assignment for content to a specific category is completely independent of where that content lives in the content structure.

• Multi-topic classification is natural and simple. Check as many or as few boxes as you want.

• There’s often a natural taxonomy or content hierarchy of categories and subcategories.

• It’s often easy to create multiple categorization schemes. You could have one category tree (or top-level branch) for “topic,” another for “format,” another for “confidentiality,” etc. Faceted classification is natural and intuitive.

• There’s rarely any control over what goes in a category. You can rarely (if ever) specify a minimum number, a maximum number, or any kind of content type enforcement. Categories are generally always a “big tent” grouping – they’ll take anything.

• Adding a category is simpler than changing the content structure to add a new content section.

• You can often delete categories without thinking enough about the content in them. If categorization is your main form of navigation, then you can orphan vast stretches of content. And since categories are often not manageable objects, there’s rarely robust permissions or versioning around then. Mistakes made here can be painful.

• You can’t usually manage permissions around categories. Few systems will let you manage who can assign Content X to what topic. Everyone can usually assign something to everything category, if they want, and this can be problematic.

• The category is often not itself a manageable thing. It often cannot carry additional data (a description, and responsible manager, etc.), it doesn’t get permissions, it isn’t assignable to workflow, and it just generally doesn’t exist in the CMS as something you can manipulate. Categories will likely also have their own API.

• It is probably not URL-addressable. If you want to list everything in Topic X on a page, then Topic X has to have a URL, and things that aren’t actual content objects might not have one. (See: Using Proxy Objects for Non-CMS Content for more on this.)

• People can get liberal with categorization, when it’s so easy. Is it at all related to Topic Y? Include it!

• On some systems, it’s not possible to specify “main” vs. “ancillary” categorization. So you can’t say, Topic X is the main place this thing lives, but it is also somewhat relevant to Topics Y and Z. This makes navigation hard. (See Of Taxonomies and Crumbtrails for more on this.)

Keywords or Tagging

This is a lot like categorization, but there’s no pre-defined structure of categories – editors just make them up on the fly. (I’ve argued in the past, in fact, that keywords and tagging differ only in interface.)

(The patterns around keywords/tagging and categorization are very similar, so all the idiosyncrasies of the that structure apply to this one as well. The following are in addition to those.)

• It’s super-casual, so editors seem to love it. They can tag with wild abandon.

• It can be way too super-casual, with people tagging stuff all over the place.

• Some really interesting aggregate patterns can emerge from tagging over time. (This concept was explored well in this book.) This is not really the operative point of using this method, just an interesting by-product.

• If there’s no central authority of tags, and no attempt to re-use tags or apply some order, then you can get massive duplication and semantic inconsistencies. (See A Problem with Tagging for more on this.)

• There’s rarely a tag hierarchy. Few systems even allow for this. (If they do, then it’s probably a category tree behind the scenes, like the relationship between Drupal’s tags and the Taxonomy module– the “tagging” of content is just an interface hack to the core taxonomy.)

• Contextual tagging can be a problem. There’s no way to tell from a tag what dimension to which it’s referring. Does “large” refer to the length of the article, or the size of the business referred to in the article? You often end up with people name spacing their tags – “length-large” – which can open up an entirely new dimension of inconsistency.

Parametric Association

This is where content happens to be in a assembly because of some property it possesses – a content type, or a value of some property ( “a parameter,” hence the name “parametric association”). No one proactively put it in the structure. Rather it got there because of what it is.

In a lot of cases, this provides an alternate, less-permanent geography that you can use for different things. It can flatten a tree, for instance.

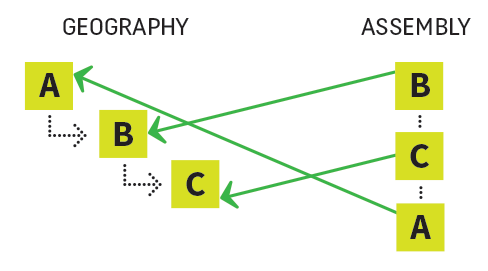
The content still “lives” in its core geography, but this particular assembly puts it in a different “shape.”

In this case, the assembly is actually a query. Most likely, the query is executed at the time of retrieval (barring any caching), and it returns the content that matches at that moment.

Perhaps you have a master news list, and something will appear on this list if it’s of the “news article” content type, no matter where it appears or what category it’s in.

• Inclusion is implicit and can be forced. If your editor adds content of Type X, then it’s going in this list, whether they want it to or not.

• Sequencing can be implicit in the property. Blog posts can not only appear in the blog section, but they can be sorted by date because date is a property which is sortable.

• It cuts across all other types of categorization. I don’t care where your news article is, if it’s a “News Article” content type, it’s going in this list. (Rarely, this can be a drawback.)

• It’s rigid and hard-baked into the content model. Changing it can be complicated. And retrieving the content often involves a query of some kind at the template level.

• It often involves relational content modeling along properties. Support for this varies widely. Not many systems do it well.

Structured Referential Assembly

This is when you define an assembly that content can be grouped into by reference.

Your CMS might have a menu system, for instance, which you populate by pointing menu nodes at content – Drupal is fundamentally defined by such a system. Ektron used to have a handy system of “collections,” which were just lists of content – you added content to the collection, and manually ordered it.

This is the most obvious example of an assembly apart from your core geography. In Drupal’s case, it draws “order out of chaos.”

The actual geography might just be a big, unordered bucket of content (the anti-geography?). However, the assembly (Drupal’s menu, in our example) takes that stuff and puts it in some semblance of order. It still “lives” in a big mass, but the assembly is how you refer to it (usually for your navigation).

But organizing any content in a serial or hierarchical assembly is simple. What’s harder is when you can specify content types and specific ways that this content has to fit together to form a valid assembly.

• They can be rudimentary and simplistic. Often being able to group content into a tree structure is just enough to get what you want done, but not much more. Often it’s lacking.

• You can usually always define ordering.

• It’s rare that you can define typing restrictions, but extremely powerful when you can. For instance, if you were assembling a magazine issue, you might want to specify restrictive “slots” in the assembly into which specific content types have to fit – an “issue” contains a “main image” and an “introduction,” then one or more “sections” each which contain one or more “articles.” This is a strongly-typed assembly, and very few systems will let you define them in this manner.

• It often overlaps quite heavily with the core content geography. But remember that this is a referential assembly of content – the content actually lives elsewhere (or in the case of a system like Drupal, it just lives in a big unstructured mass, and the menu system is the core way you’re expected to structure it). So, if you have a content geography yet you run your navigation off a referential assembly…it can get confusing.

• Referential assemblies can often be properties of other content objects. Many systems have a “Link List” or something similar as a property type, which means you might have to have a content objects for no reason other than to have a referential assembly as one of its properties.

There’s a lot of absorb here, and knowing which assembly type is the right one to use is purely a process of (1) experience (by painting yourself into a corner by picking the wrong method too many times), and (2) intimate knowledge of your particular CMS and what it offers.

You don’t find many sites of any significant size using just one method of assembly. Most sites use dozens, and there’s often confusion between the methods – you do use Method X for Menu X and Method Y for List Y and Method Z for Topic Page Z. Except on every simple sites, it often gets messy quickly.

Sadly, There is no Grand Unified Theory of Making Stuff Appear Together in Some Location.

If only.